コレクション 比 求め方 3�� 728666-比 求め方 3つ

 3つ以上の比 346といった3つの数の比は、それらの数の最小公倍数をまずは計算します。 この場合は12です。 (3,4,6)=12 この最小公倍数で3つの数を割ります。 3→4 4→3 6→2 割ってでてきた数を並べた432がもとの比の逆比になります。 連比 上で見た「比」は2つの数を比べていましたが、3つ以上の数を比べることもあります。例えば\ 345 \と比べることもあります。これも「比」と呼びますが、特に「 連比 」と呼ぶこ では、構成比がどのようなものか整理したところで、エクセルでの求め方です。 構成比を求める計算式は、 「構成比を出したいセル」 ÷ 「全体の値」 構成比を出したいセルを、全体の場所で割り算してあげると出てきます。 下の表の「構成比」の場所を求めてみます。 まず、表の内容を確認してください。

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

比 求め方 3つ

比 求め方 3つ-AD＝3cm、BC＝9cmなので、相似比は1：3です。面積比は相似比の2乗です。つまり、面積比は1：9です。 OADの面積は12cm 2 なので、以下の比例式を作ることができます。 $19=12x$ この比例式を解くと、以下のようになります。 $x=9×12=108$相関比は, 0～1 の値となります。 相関比は判別的中率同様に, いくつ以上あればよいという基準はありませんが, 筆者は05 を基準の値としています。 この例題の相関比は0674 で05を上回ったので、関係は予測に適用できると判断します。

平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

また、2つの比だけでなく3つの比が等しいことも比例式で表せます。 \( ab=cd=ef\) ･･･① または \(\displaystyle\frac{a}{b}=\frac{c}{d}=\frac{e}{f}\) ･･･② のように3つ以上の比が等式で結ばれたものを「 連比 」といいます。先ほどの問題で実感した通り、3つの辺の長さを求めないと三角比の値が分かりませんでしたね。 しかし、この章のタイトルにあるように 30°、45°、60°を基準と考えた直角三角形では 辺の長さを求めずとも三角比の値を求めることができます。 3つ以上の比のしくみがわかりません。 ab=34 ac=23 を3つの比にするとabc=6に説くことはできます。 しかしどうしてこのようなことが成り立つのかわかりません。 意味を理解したいので解き方ではなく理由を教えてください。

比を簡単にする手順 まず比の2つの数に対する最大公約数を求めます。 次にそれぞれの数を最大公約数で割ることで比を簡単にできます。 12：18 → 12と18の最大公約数は6 → 12÷6：18÷6 → 2：33つの比 a：b：c＝1：2：3 のような比の問題を解いてみましょう。 例題 a：b：c＝2：3：4のとき、a／2＝b／3＝c／4 となることを示してください。 a：b＝2：3 から、3a＝2b 両辺を6でわると、 a／2＝b／3 ・・・① b：c＝3：4 から、4b＝3c 両辺を12でわると、 b／3＝c／4 ・・・② ①と②から、a／2＝b／3＝c／4 一般に、つぎの規則が成り立ちます。 規則 a：b：c＝x：y：z ⇔比の計算の解説 比は、その比に同じ数を掛けるか割った別の比と同じという性質を持っています。 12 = 24（左の比に2を掛けたのが右の比） 36 = 12（左の比を3で割ったのが右の比） 比の関係は分数の関係によくにています。 分数の場合も、分母と分子に同じ数を掛けるもしくは割った分数と同じです。 約分したら同じ分数になるということですね。 1 2 =

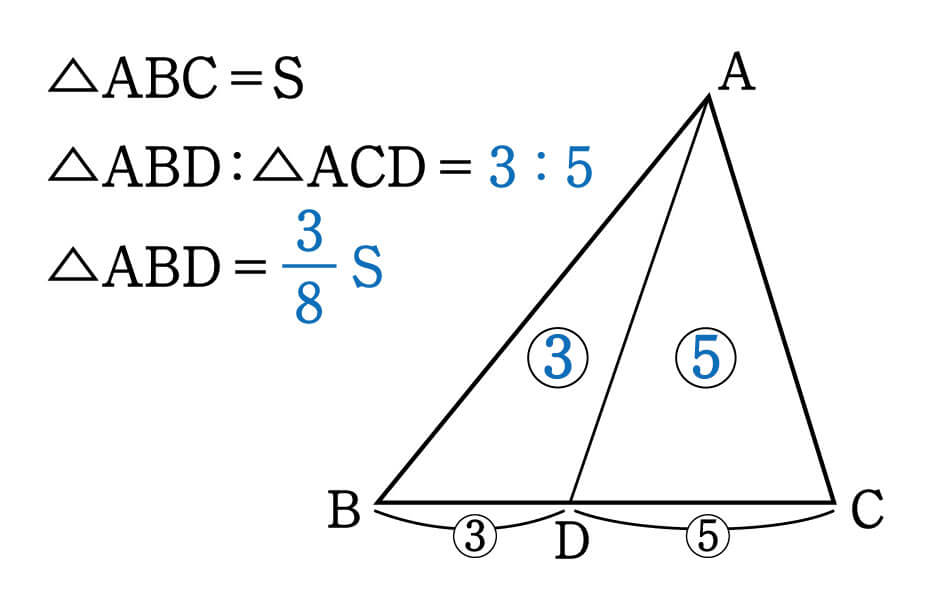
 計算式 構成比 = (カテゴリー/項目/要素) ÷ 全体の売上高 構成比率 (%) = (カテゴリー/項目/要素) ÷ 全体の売上高 x 100 例 例えば、ABスーパーに"肉屋""魚屋""米屋"があったとします。 ABスーパーの今月の売上高は、2,000,000円でした。 肉屋は850,000円、魚屋は550,000円、米屋は600,000円でした。 その時の各構成比を計算してみます。 肉屋 = 850,000円 ÷ 2,000,000円 = abという比率の求め方 このようなExcelシートを例にします。 セルB1・B2それぞれに、比率を求めたい2つの数値を入力します セルE2は、比率が出力される場所です 比率を求めるために、セルE2には以下の式を入力してください。 =B1/GCD(B1,B2) & "：" & B2/GCD(B1,B2)面積比の求め方を理解しよう こちらの記事で説明したように、 三角形の面積比は「（底辺の比）×（高さの比）」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。

中学数学 相似比の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

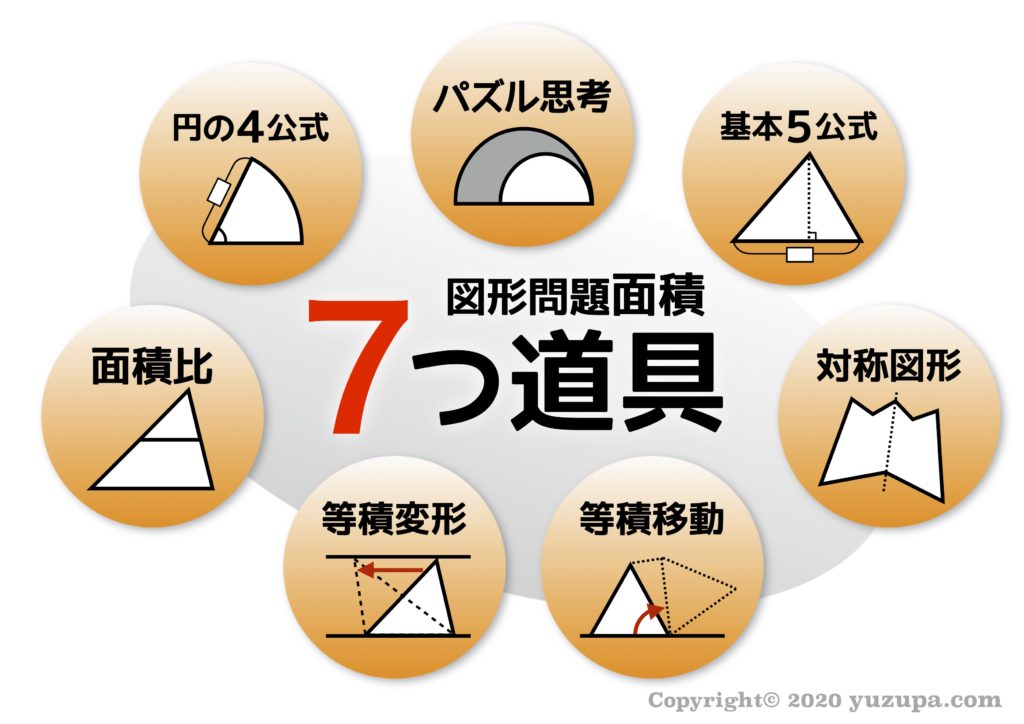
中学受験 図形の面積問題は ７つ道具 で攻略 かるび勉強部屋

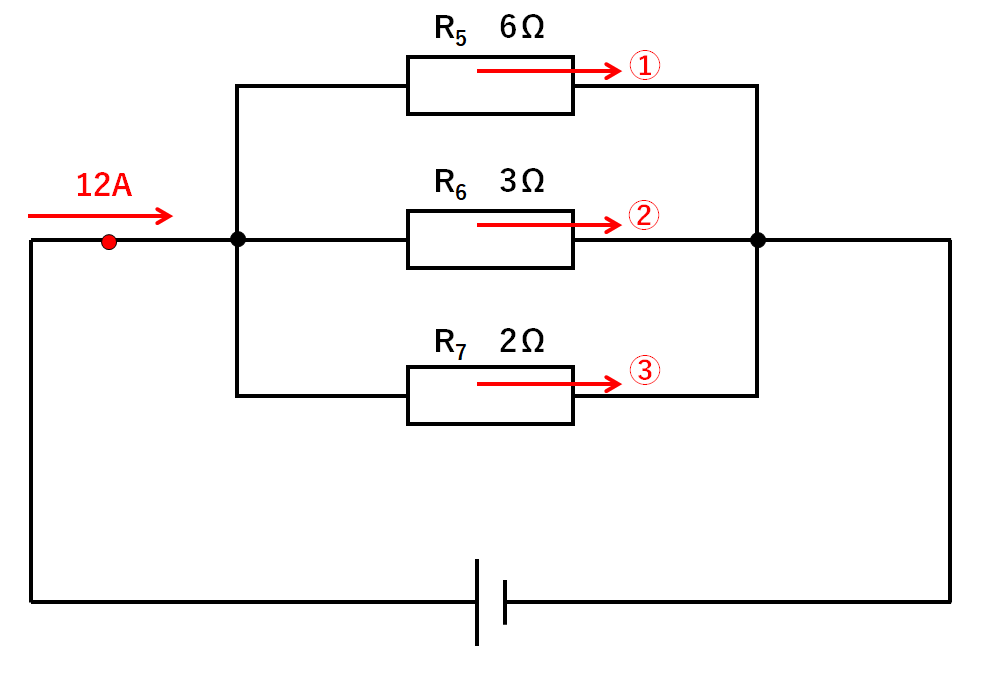
 「(a さんが折った鶴の数) (b さんが折った鶴の数) \(= 7 9\)」だけでは問題を解けません。 \(2\) 人の合計の比も入れた「連比」を立てるのがポイントです。 連比をなす \(3\) 項からどの \(2\) 項を取り出してもその比はくずれない ことを利用して、a さん、b さんの鶴の数を順番に求めまパーセントの意味を図解で分かりやすく解説 「パーセント」というのは「百分率」で求められる単位です。 では「百分率」とは何かと言うと、全体を "100" とした時に、対象のものがどれくらいなのかを表します。 少し違う言い方をすると、『全体を100個に分けた時、対象のものはいくつか？ 4/5=4÷5=08Ωが求められます。 和分の積 分母を足し算（和） 分子を掛け算（積） 並列接続された抵抗の合成抵抗を求めらることができます。 3つ以上の並列抵抗ではそのまま当てはめることはできません 回路の全電流は12V÷08Ω= 15A と求められます。

数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

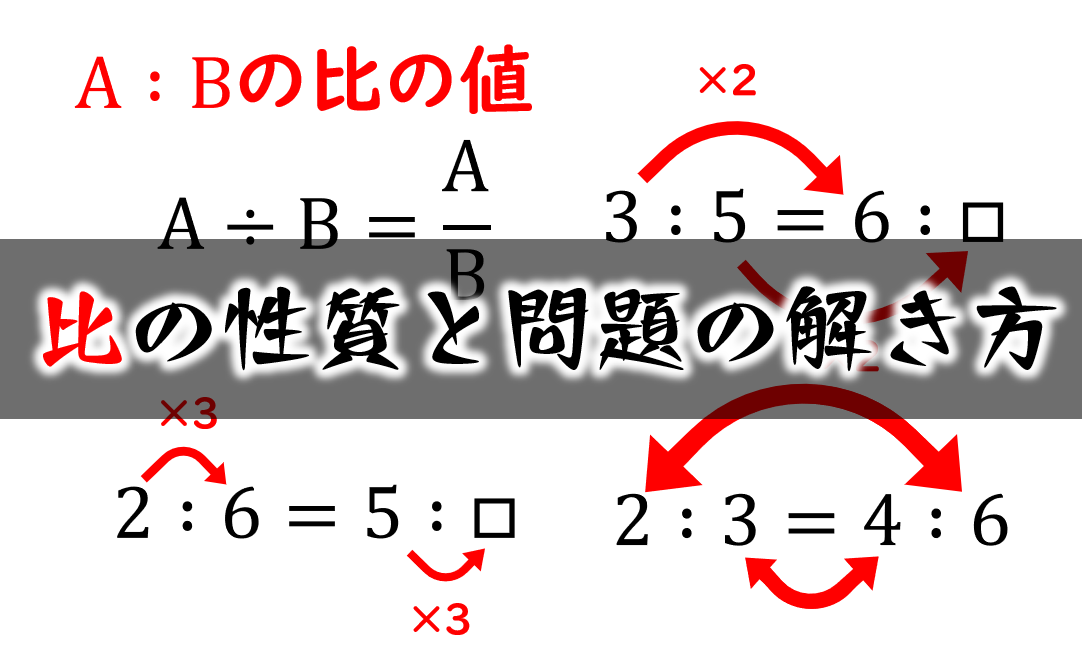
比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

 比の3つのポイント 比例配分、連比、逆比 1、比例配分は合計にあたる比を考える 兄と弟で1000円を73に分けたときいくらずつ分けましたか。 という問題。比は割合と同じく何倍か なので兄は7倍、弟は3倍のお金をもらったという意味。だれの？2つの異なる比、つまり2種類の記号がでてきたら・・・ 今回なら〇と だけど。 B＝⑤＝ 3 のように2つの比の共通部分を公倍数でそろえて、1つの比（1つの記号）ににしてしまうのが連比という解法だったよね。 この当たり前の事実を復習した上で 今回は小学6年生で習う「比とその利用」について勉強します。 比の性質を使い、整数だけでなく小数や分数の比を簡単にする方法について学んでいきたいと思います。 比を簡単にする方法 比を簡単にする問題 問題① 問題② 問題③ スポンサードリンク (adsbygoogle = windowadsbygoogle )

６年算数比とその利用２等しい比の教え方

世界一分かりやすい算数 小６ 比とその利用

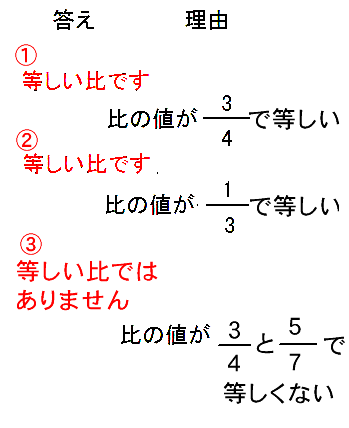
 今回は、比の値の求め方について書いていきたいと思います。 比の値とは？ 比の値を求める問題 問題① 問題② 問題③ 比の値とは？ a：bという比があったとき、前項aを後項bで割ったが比の値になります。比の値＝前項÷後項後項を1としたときに、前項がどのくらいにあたるのかを表し 比についての問題は本当にたくさんあるのですが今回はその基本となる比の操作について記事にしました。 比の操作で特に重要なのは次の3つです。 「比例配分」「連比」「逆比」 この中で習うときには最も簡単で、使いこなすのは最も難しい「逆比」について触れたいと思います。 逆比とは比をそれぞれ逆数にしたもののことです。 ただそれだけなんで比例式ツール。 3箇所に数値を入力すると残り1箇所のを計算します。 比例式（ひれいしき）とは、比あるいは連比に関する等式のことである。 A に対する B の割合が、X に対する Y の割合に等しいとき、 AB=XY と書く 引用： 比例式について wikipedia 用途

平面図形をマスター 三角形の面積比 応用編その３

平面図形をマスター 三角形の面積比 応用編その３

43 少数と分数から整数比を求める問題 431 少数を整数に;このような、a：b＝c：dという比の式を比例式といいます。 3．比を図形を使ってわかりやすく説明 外項の積、内項の積数といわれてもよくわからないと思いますので、比をわかりやすく理解するために図形を使って説明します。 下に2つの四角形があります。ウルトラフリーダム Just another WordPress site

小学６年生 算数 9月 比の性質 比の求め方 比の利用 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ

比の計算問題を実践練習

 比が割合と違う点は、3つ以上の数字を比べることができるという点です。 ただ3つ以上の数字でも比を簡単にする手順は変わりません。 比を簡単にする手順 （小数や分数の場合）整数にする 公約数を見つける それぞれを公約数で割る 問題3 に入る数字を求めよ （1） 3：5＝6： 3 ： 5 ＝ 6 ： 答えを表示 （2） 2：6＝5： 2 ： 6 ＝ 5 ： 答えを表示 （3） 9：12＝ ：4 9 ： 12 ＝ ： 4 答4 比の計算問題 41 最小の整数比を求める基本問題;3つの数の比率と計算は？計算方法 3つの数の比率を下式に示します。 abc=123 上式のように、3つの数を比率で表しています。2つの数の比率に比べて少し複雑ですが、慣れると簡単です。 3つの数の比率は、下記のことがいえます。 abc=123 ab =12 bc=23

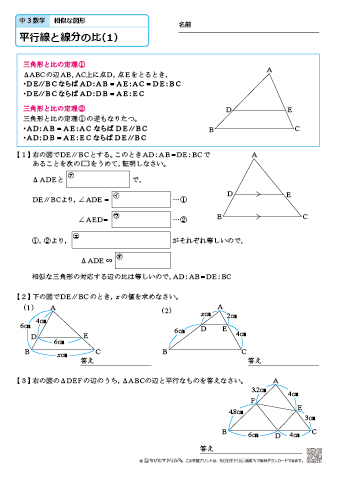
中学３年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

６年算数比とその利用２等しい比の教え方

集合問題でベン図を使って解きなさいという問題はあまり見ませんが、 実はベン図を使うと楽に求めることができる問題は少なくありません。 要素が2つの場合は小学生や中学生でも使うでしょうが3つの場合の解き方もあります。 ここで 比と前項（後項）の値から後項（前項）の値を求めることができる。 評価規準 比の性質や図を用いて比の一方の値を求める方法を考え、説明している。（数学的な考え方） 問題 ケーキを作るのに、砂糖と小麦粉の重さの比が5：7になるように混ぜます。使い方 「値の数」を選択してください。 「値1」「値2」「値n」欄に、比率を算出したい値を入力してください。 値の変更・基準の変更・Select Boxの変更などを行うと自動的に算出します。 「基準」を任意の項目に変更すると、その値を100として、他の値を計算しなおします。 とりあえず実行したい場合には、サンプルリストから任意の項目を選んでみて

3

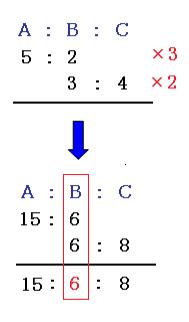
比の性質を解説 比例式や連比の解き方だってこんなに簡単

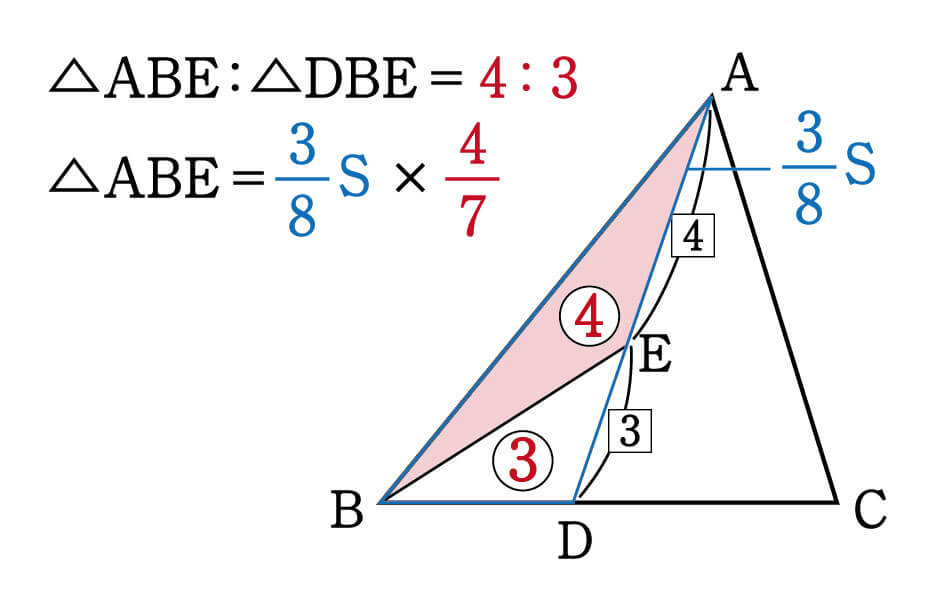
3 比の計算方法 31 比の表記ルール; 2 主な同位体の「存在比」 3 存在比から元素の原子量を求める方法; 1つ目のステップでは、 ABDと ACDの面積比に注目します。 隣り合う三角形の①の型なので、底辺の比＝3：5から面積比も3：5。 そして左側の ABDは、 ABCを8等分したうちの3つ分ですから、\( ABD\)の面積＝\(\displaystyle \frac{3}{8}S\)と表すことができます。

中学受験 割合と比は ７つ道具 で克服 かるび勉強部屋

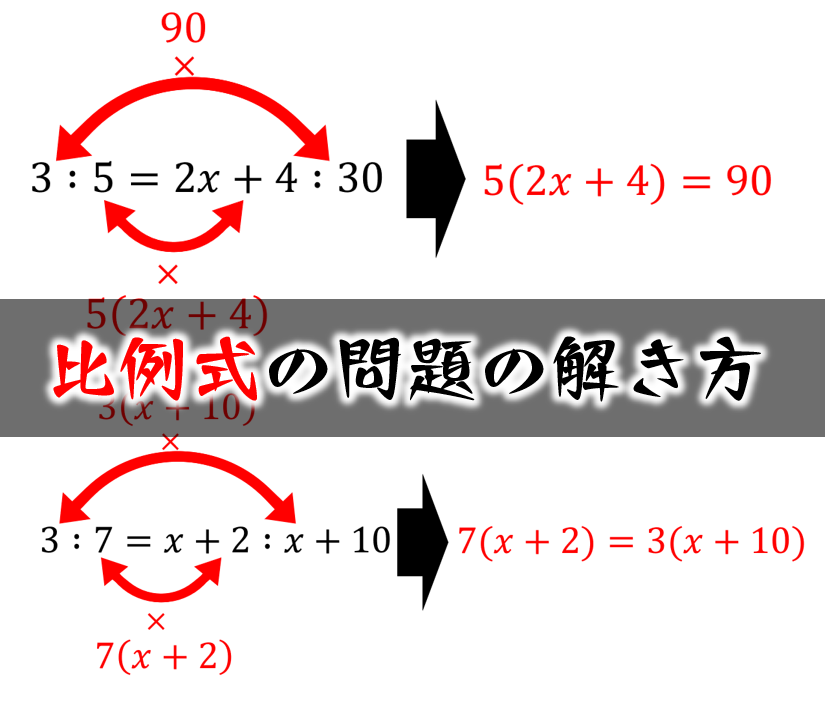
比例式の問題の解き方 数学fun

比例式とは12＝24のように、数の比を等式で示したものです。 2つの比だけでなく、3つの比を等式で表すことも可能です。 また比例式ab=cdは、ad=bcに変形できます。 例えば12=24⇒1×4＝2×2ですね。 今回は比例式の意味、問題と解き方、3つの比の計算、比例式と分数の関係について説明します。 「比」の計算、3つの数の比は下記も参考になります。 比率とは？ 1 「比が等しい」ということと「比の値が等しい」ということは同じです。 よって、①の式$$21=x3$$を$$\frac{2}{1}=\frac{x}{3}$$と変形することができます。 あとは両辺に $3$ をかければ$$x=6$$と解くことができますね。

構成比率は全体の何 の前に 大きい数で割る感覚を鍛えなさい Excel割合の問題 就職活動 わえなび ワード エクセル問題集 Waenavi

比の計算はこれで完璧 比の値の求め方と考え方

比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

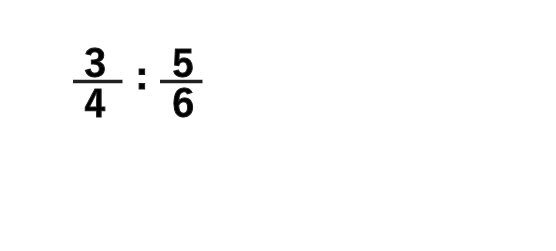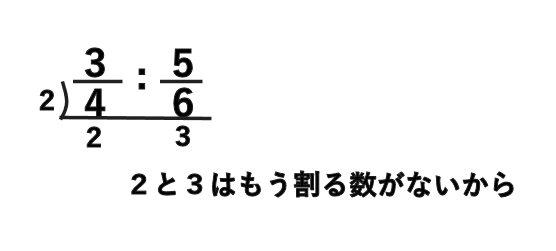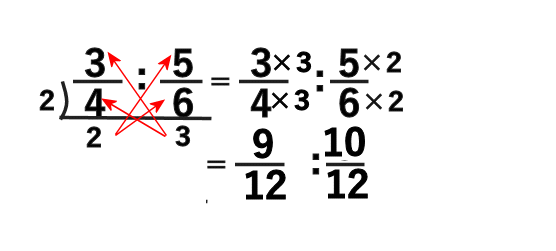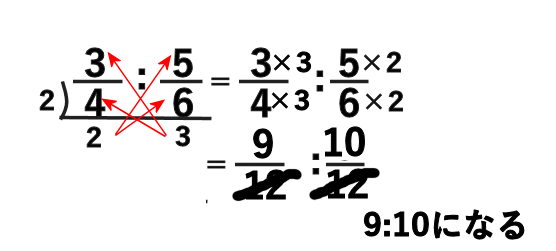
分数の比を簡単にする

黄金比の求め方 世界で最も美しい比率 数学の面白いこと 役に立つことをまとめたサイト

数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく

中学受験 割合と比は ７つ道具 で克服 かるび勉強部屋

中学受験 割合と比は ７つ道具 で克服 かるび勉強部屋

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

1

比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

小6 比 比の計算 比を用いて面積を求めよう 日本語版 Youtube

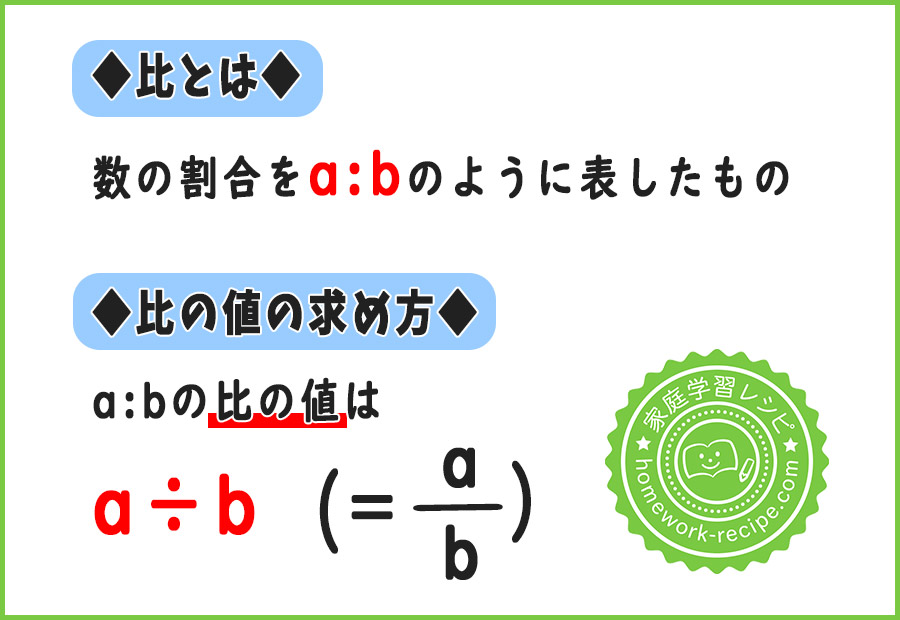
比と比の値についての自主学習ノート例 家庭学習レシピ

中1数学 比と比例式 比の値 とはなんだろう Qikeru 学びを楽しくわかりやすく

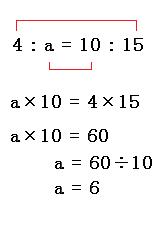
比の性質を解説 比例式や連比の解き方だってこんなに簡単

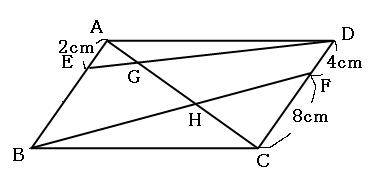
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

中学受験 割合と比は ７つ道具 で克服 かるび勉強部屋

比率 何対何 に関する計算のやり方 具体例で学ぶ数学

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

小６ 算数 小６ １６ 比と比の値 Youtube

中2物理 抵抗の比と電流 電圧 中学理科 ポイントまとめと整理

すきるまドリル 小学６年生 算数 比と比の値 比と比の利用 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント

比を簡単にする Youtube

三平方の定理の公式とは 証明から計算問題まで紹介 辺の比と角度一覧表も テラコヤプラス By Ameba

内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学

1

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

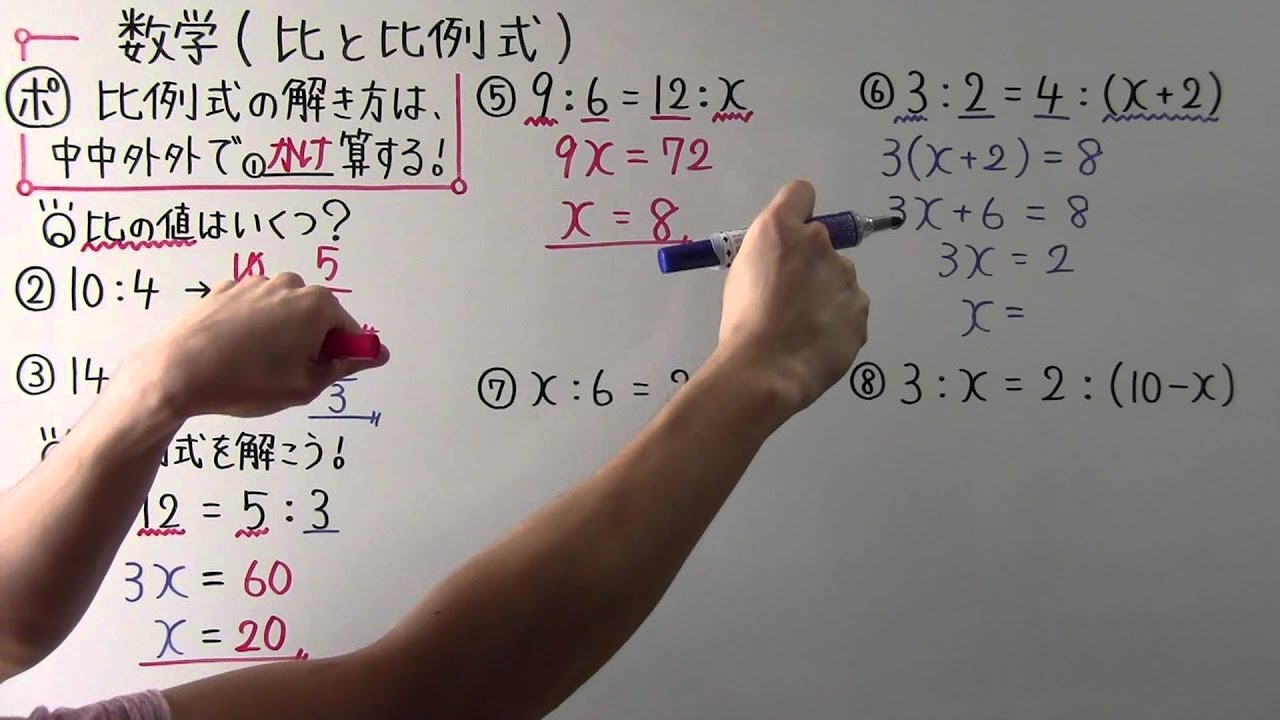
中１ 数学 中1 32 比と比例式 Youtube

倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座

算数小６の問題です 分数の比を簡単にするという問題です ６ Yahoo 知恵袋

直列回路の電圧の求め方 比例配分の利用 なるほどの素

公倍数 最小公倍数の簡単な求め方 ３つ以上の数 算数パラダイス

数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

比の値の求め方 小学生 中学生の勉強

６年算数比とその利用２等しい比の教え方

数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

歯車

６年算数比とその利用２等しい比の教え方

比の性質を解説 比例式や連比の解き方だってこんなに簡単

苦手意識があっても大丈夫 流水算の基礎でつまずかない考え方とは

平面図形をマスター 三角形の面積比 応用編その３

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

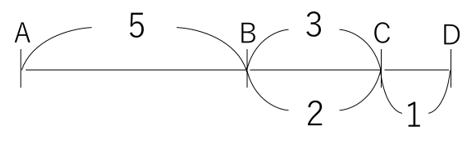
目で見てわかる 比あわせ 中学受験プロ講師ブログ

重量比 配合比 の計算を行う方法 問題付 ウルトラフリーダム

直列回路の電圧の求め方 比例配分の利用 なるほどの素

3 の求め方がわかりません どなたか回答宜しくお願い致します Clearnote

比と比の値についての自主学習ノート例 家庭学習レシピ

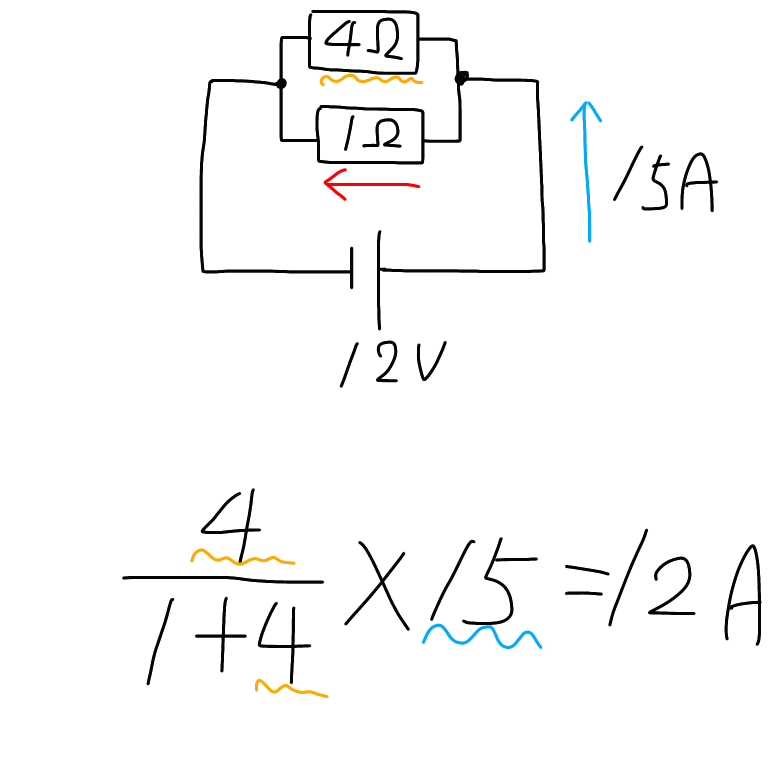
簡単な求め方 並列接続時の電流の分流について 電子の部屋

下のsin8 Cos8 Tan8の求め方 解き方1からになりますが教えてくだ Clearnote

比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

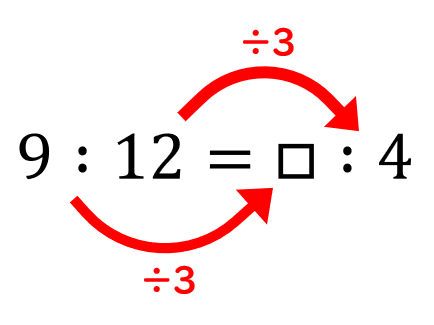
比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

構成比率は全体の何 の前に 大きい数で割る感覚を鍛えなさい Excel割合の問題 就職活動 わえなび ワード エクセル問題集 Waenavi

６年算数比とその利用２等しい比の教え方

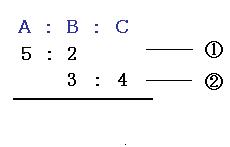
比の性質を解説 比例式や連比の解き方だってこんなに簡単

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

小学5年生 割合の簡単な求め方は くもわ 公式より分かりやすい出し方 無料プリント そうちゃ式 分かりやすい図解算数 別館

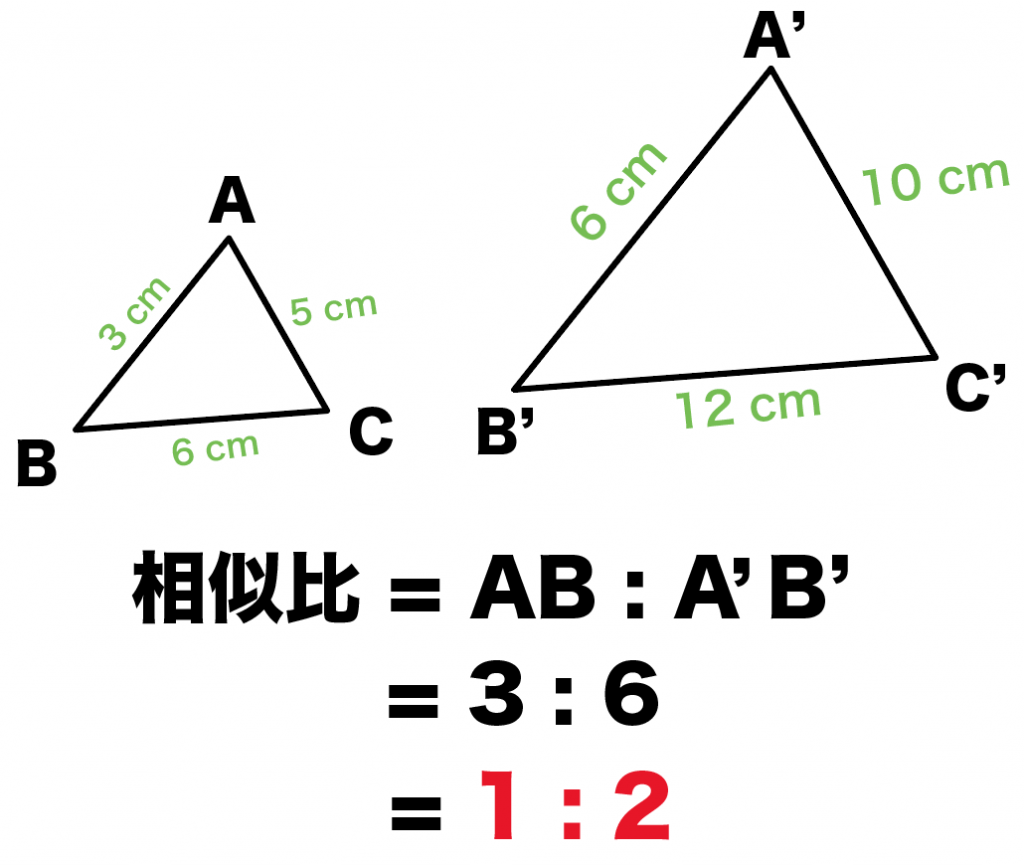
3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

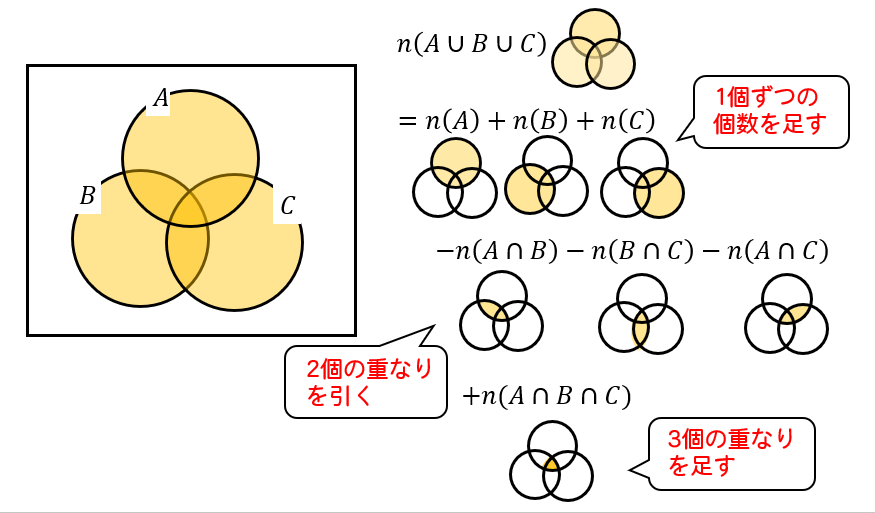
3つの集合の要素の個数 イメージ図を使いながら求め方を解説 数スタ

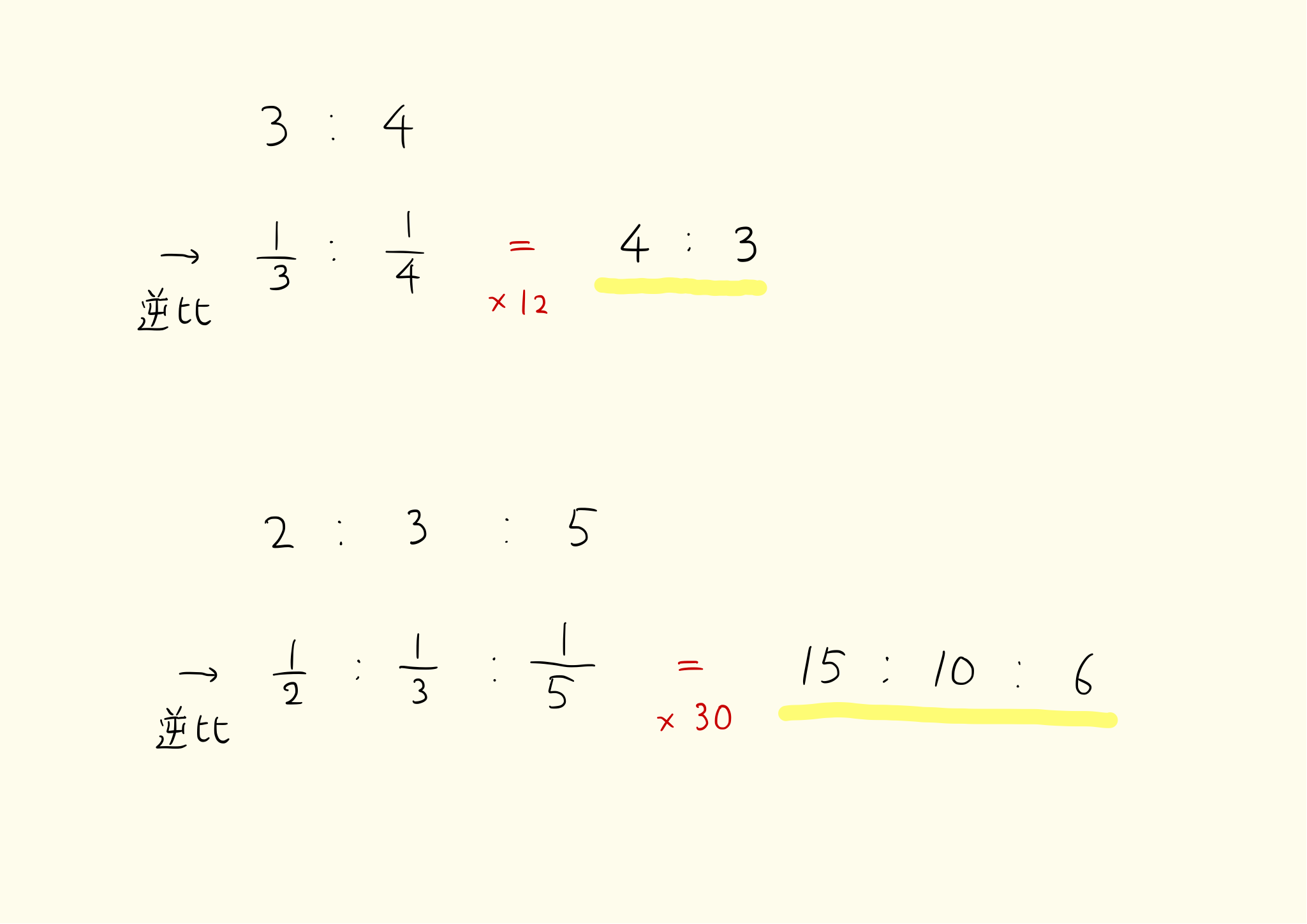
逆比の例と計算 分数 小数 3つ以上の数の比の逆比 中学数学 Irohabook

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

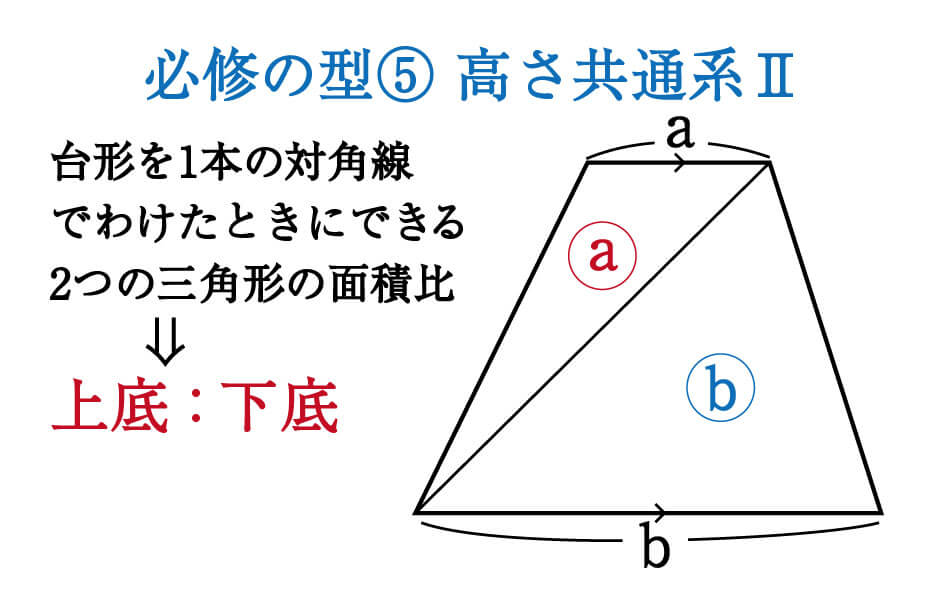
数学 対角線の入った台形 一角共有の三角形 面積比 集中特訓 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

平面図形をマスター 三角形の面積比 応用編その３

歯車

三角形の面積比を解説 平面図形が苦手な人でもわかりやすい解き方 基本編 中学受験ナビ

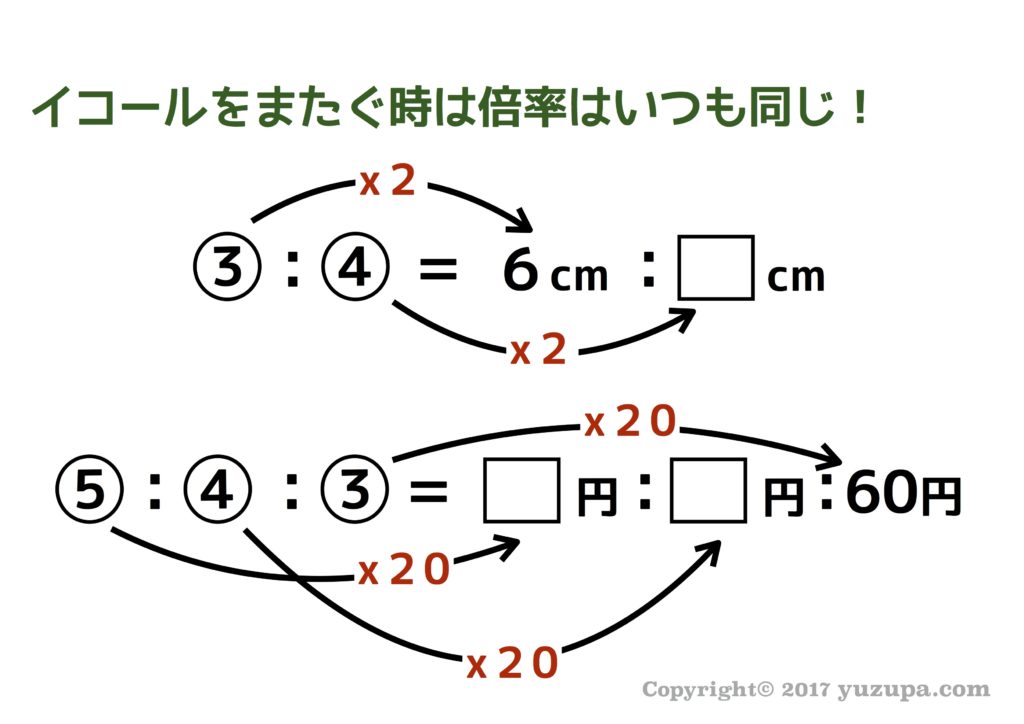
中学受験 割合と比は ７つ道具 で克服 かるび勉強部屋

1

歯車

比についての自主学習ノートの例を もう１つご紹介します 前回 比の値を求めて 等しい比を見つける練習問題をやりました 比と比の値 A B という 比で 比の値は A B で求 学習ノート 学習 小学校 算数

フィボナッチ数列を完全攻略 一般項の求め方や階段の上り下り問題を解説 テラコヤプラス By Ameba

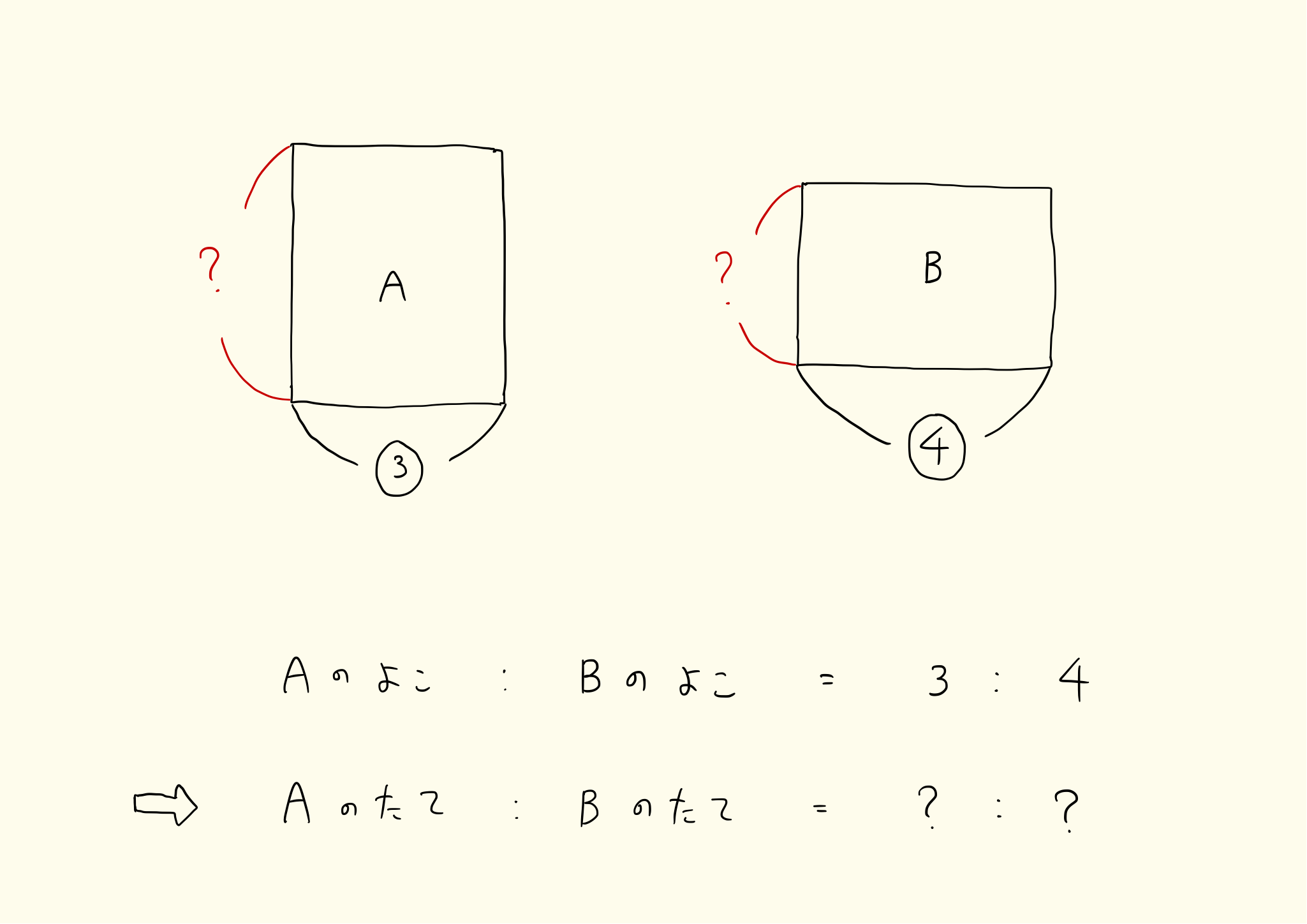
逆比の例と計算 分数 小数 3つ以上の数の比の逆比 中学数学 Irohabook

比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

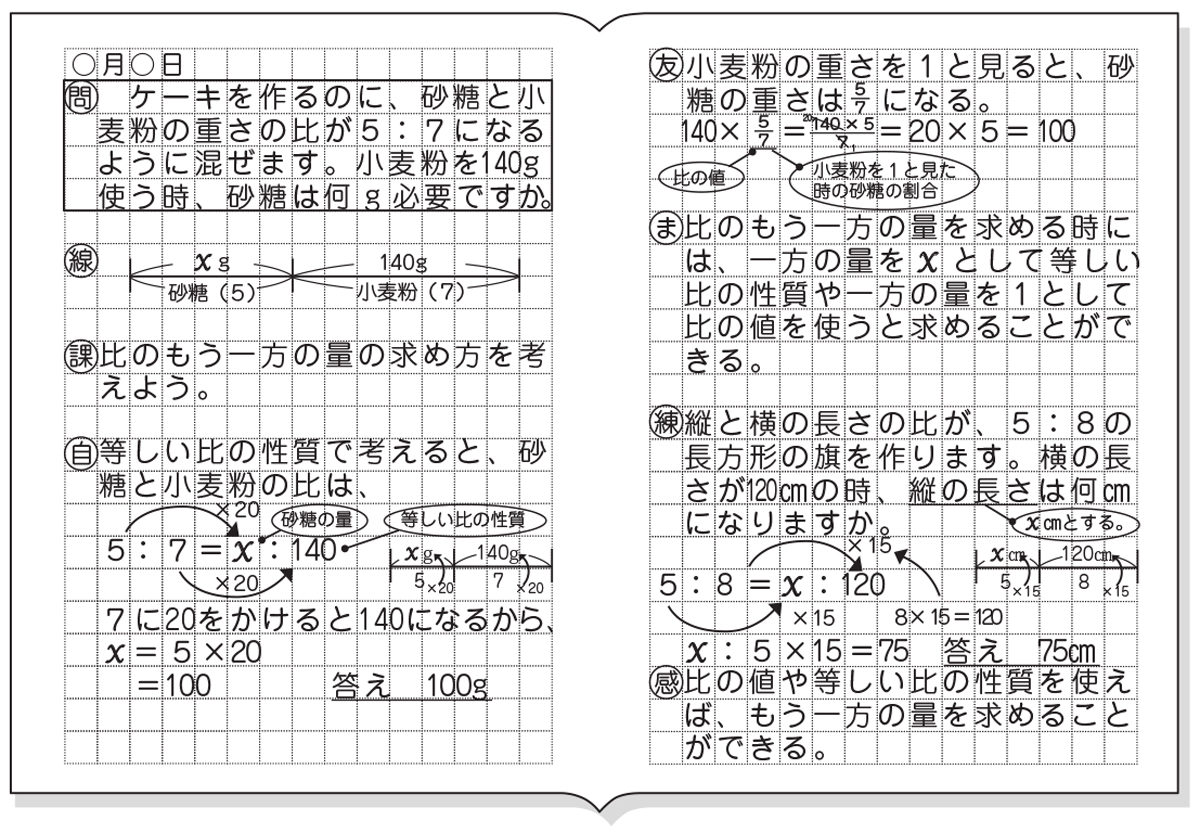
小6算数 比と比の値 指導アイデア みんなの教育技術

Excel エクセル での前年比や伸び率の計算式 前月比や前期比の求め方 Prau プラウ Office学習所

中学数学 相似比の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

比率の計算

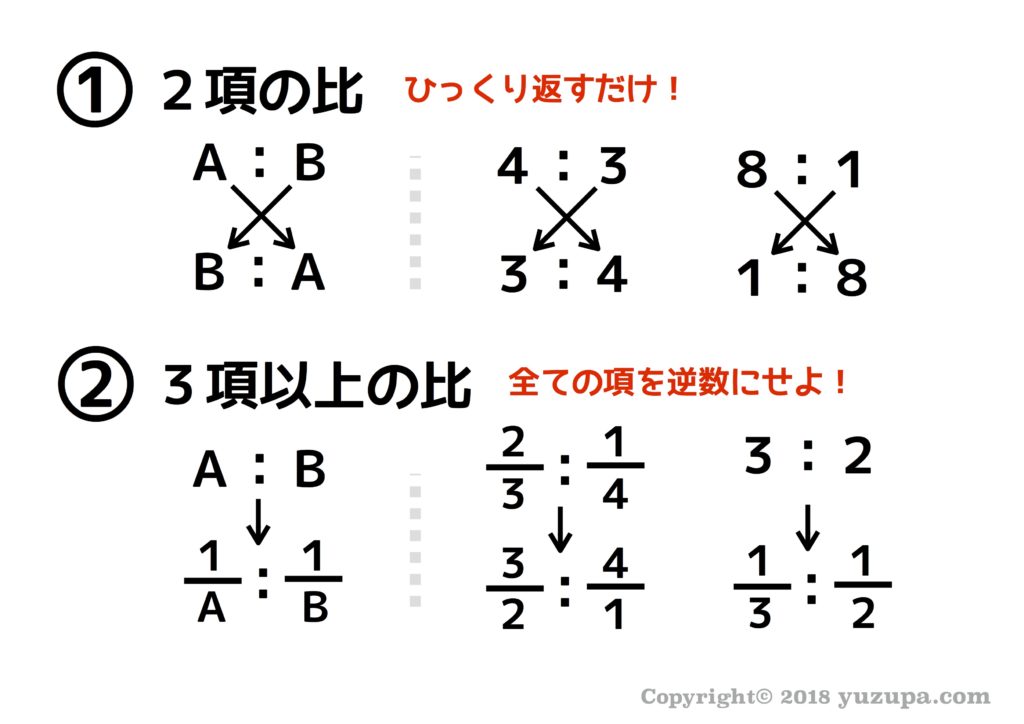
中学受験 逆比が使えるパターンは円形図で分かる かるび勉強部屋

比の計算問題 比を簡単にする方法は小学生でもできる 中学や高校の数学の計算問題

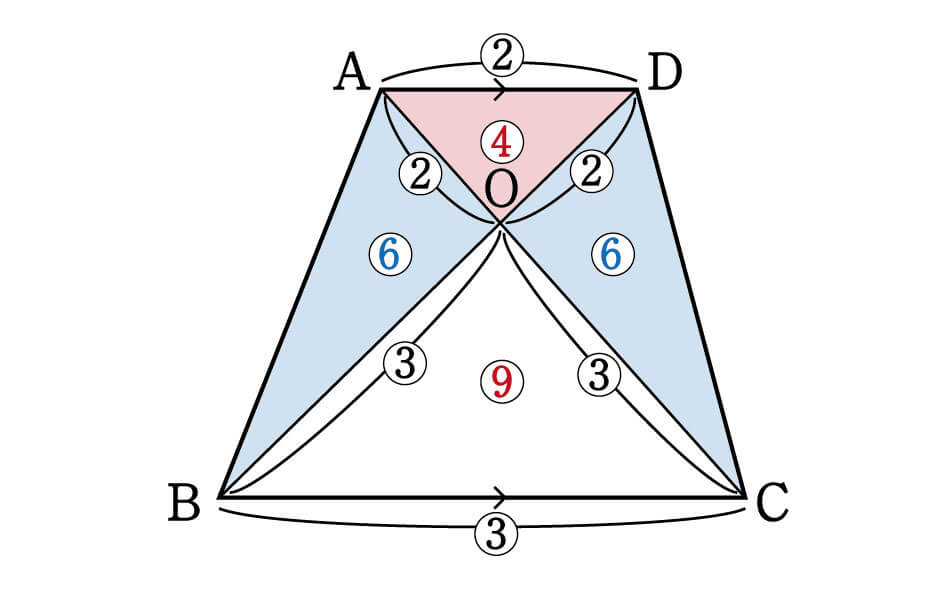
数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

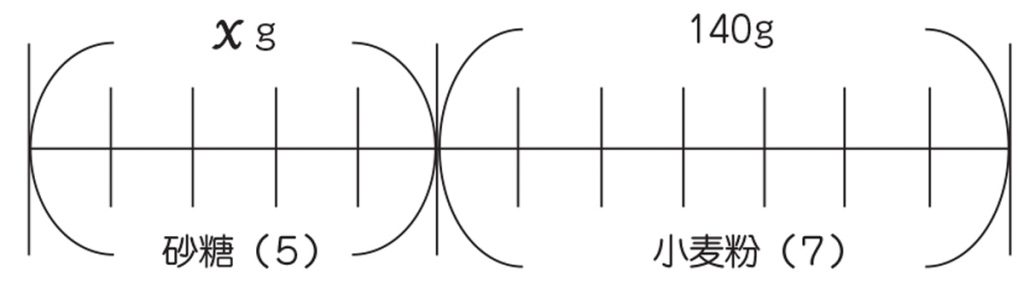
小6算数 比と比の値 指導アイデア みんなの教育技術

比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

中3 三角形の相似 円錐の体積比 日本語版 Youtube

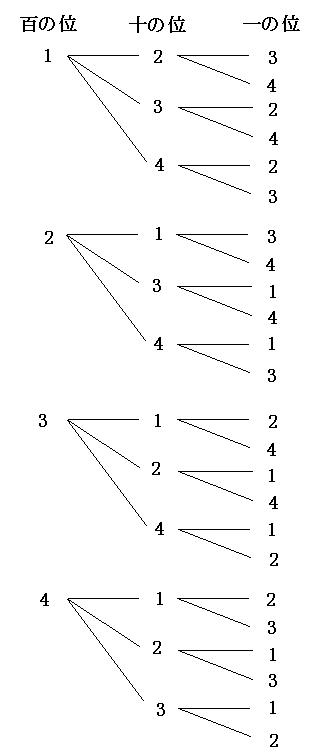
解き方解説 場合の数を計算で解く 場合の数は計算でサボれ

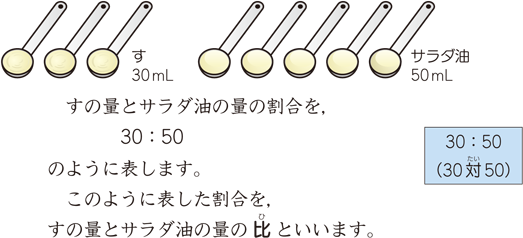
比と比の値 算数用語集

Incoming Term: 比 求め方 3つ,